Un día redondo

El jueves fue mi último día π en mi centro. Llegué en el curso 2012-2013 y me voy con sensación de haber crecido profesionalmente; siempre he pensado que lo mejor de mi centro es el alumnado y la verdad es que mi alumnado me lo ha puesto muy fácil durante estos doce años.

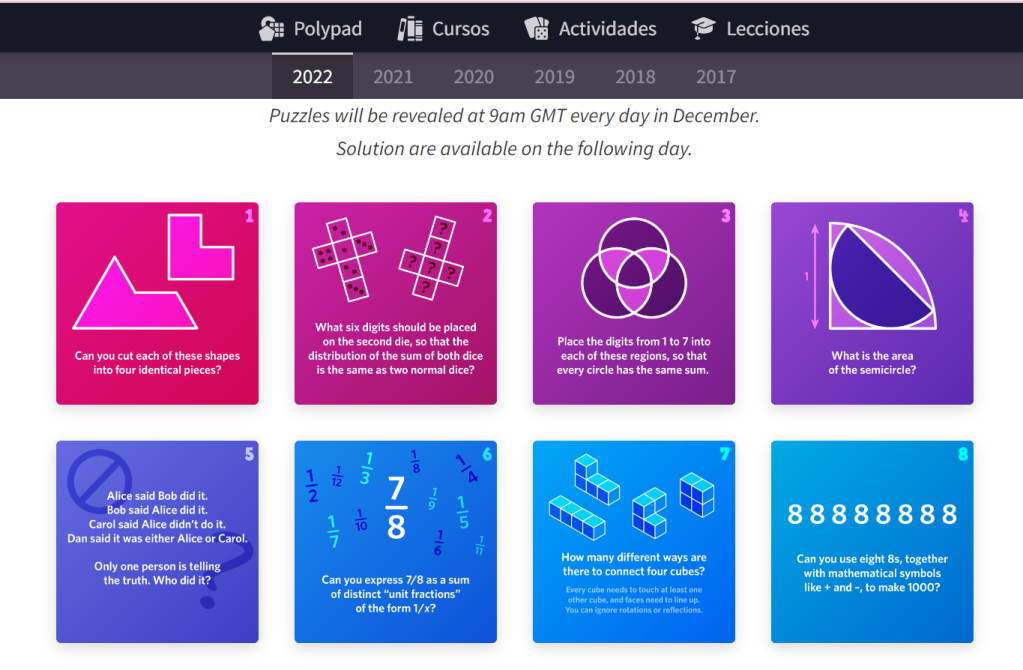
Este curso propuse a mi alumnado de Matemáticas aplicadas a las CC SS II una dinamización de recreos para celebrar el Día Internacional de las Matemáticas. Se establecieron grupos para la realización de las actividades, que se recogían en este cartel :

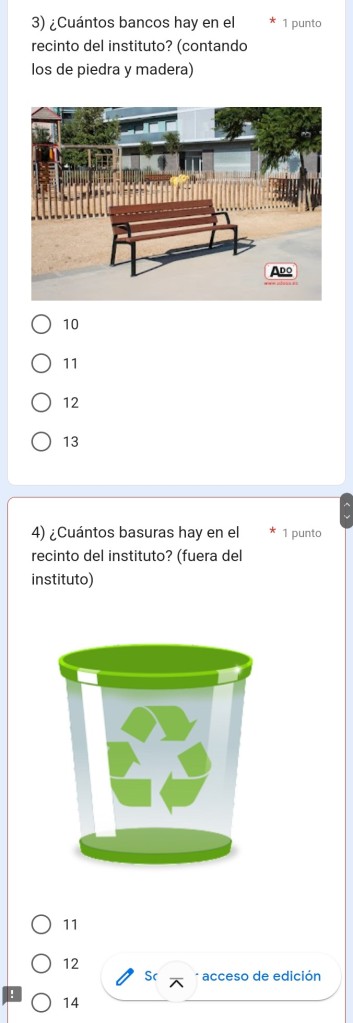
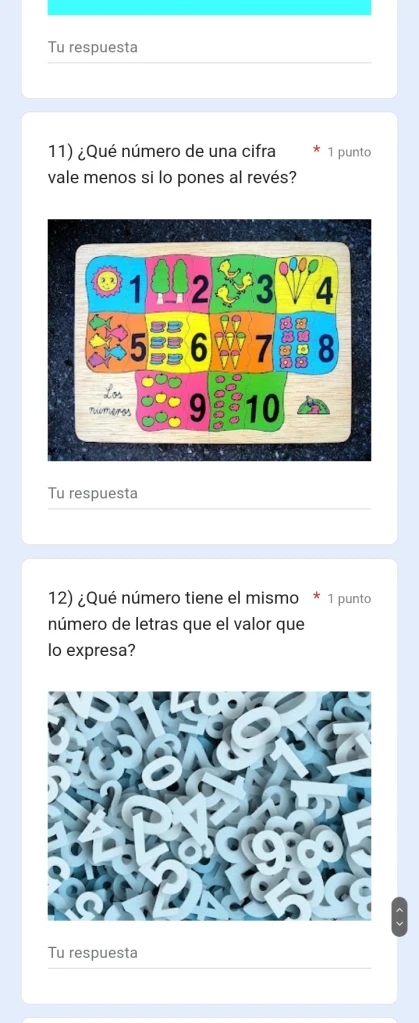
Una parte del alumnado diseñó un formulario para que pudiera realizarse en ambos recreos. El código QR para acceder al formulario se encontraba en carteles físicos en el centro y se difundió en la red social Instagram.

Otro equipo organizó el concurso de circunferencias en el patio y la construcción gigante del número π

View this post on Instagram

A post shared by IES María Telo (@iesmariatelo)

Durante los dos recreos Yerai y Valentina realizaron entrevistas al alumnado .

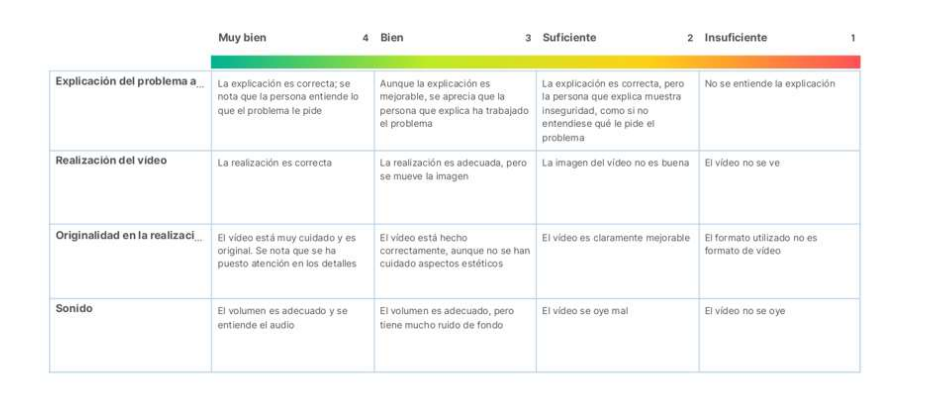
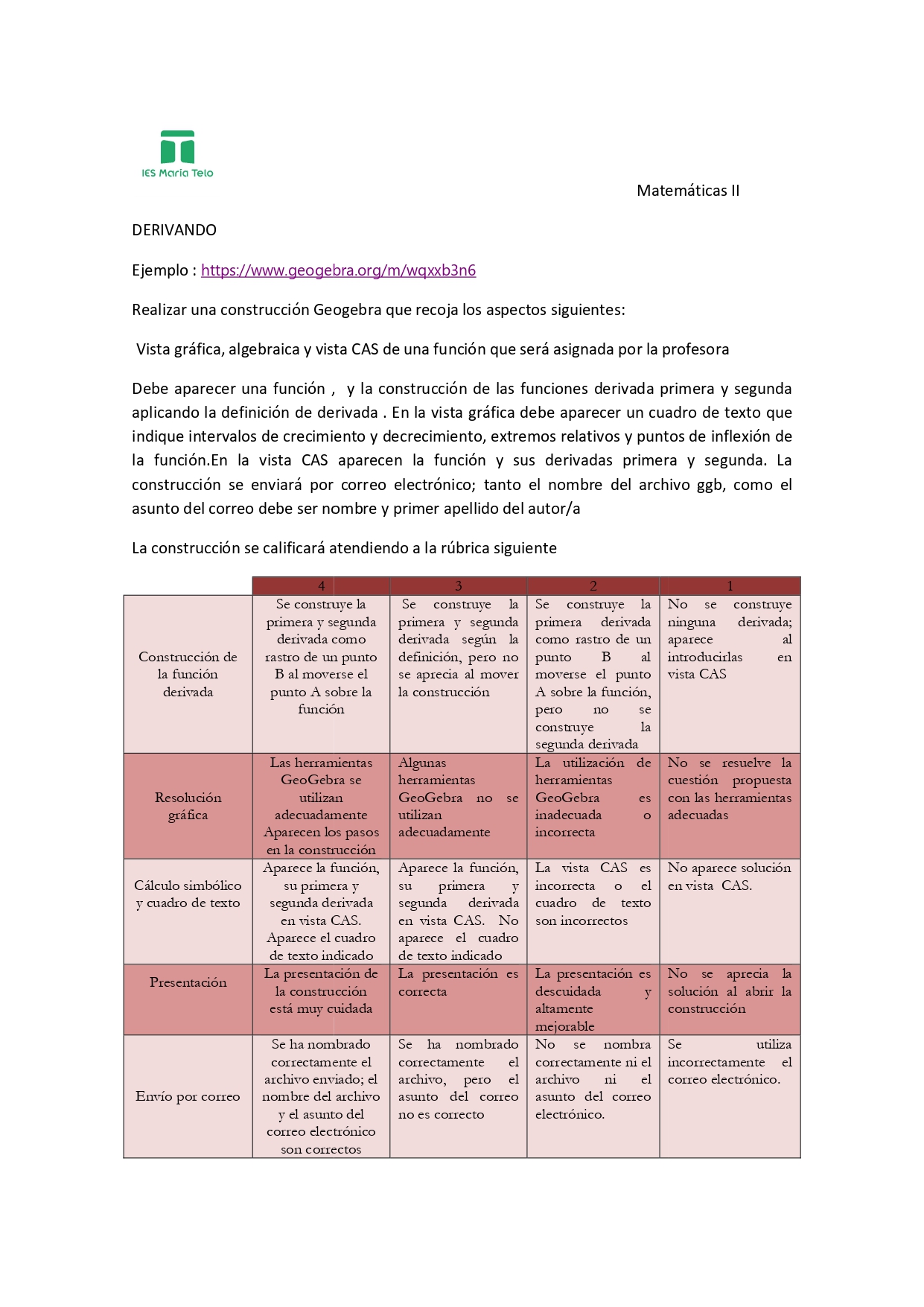
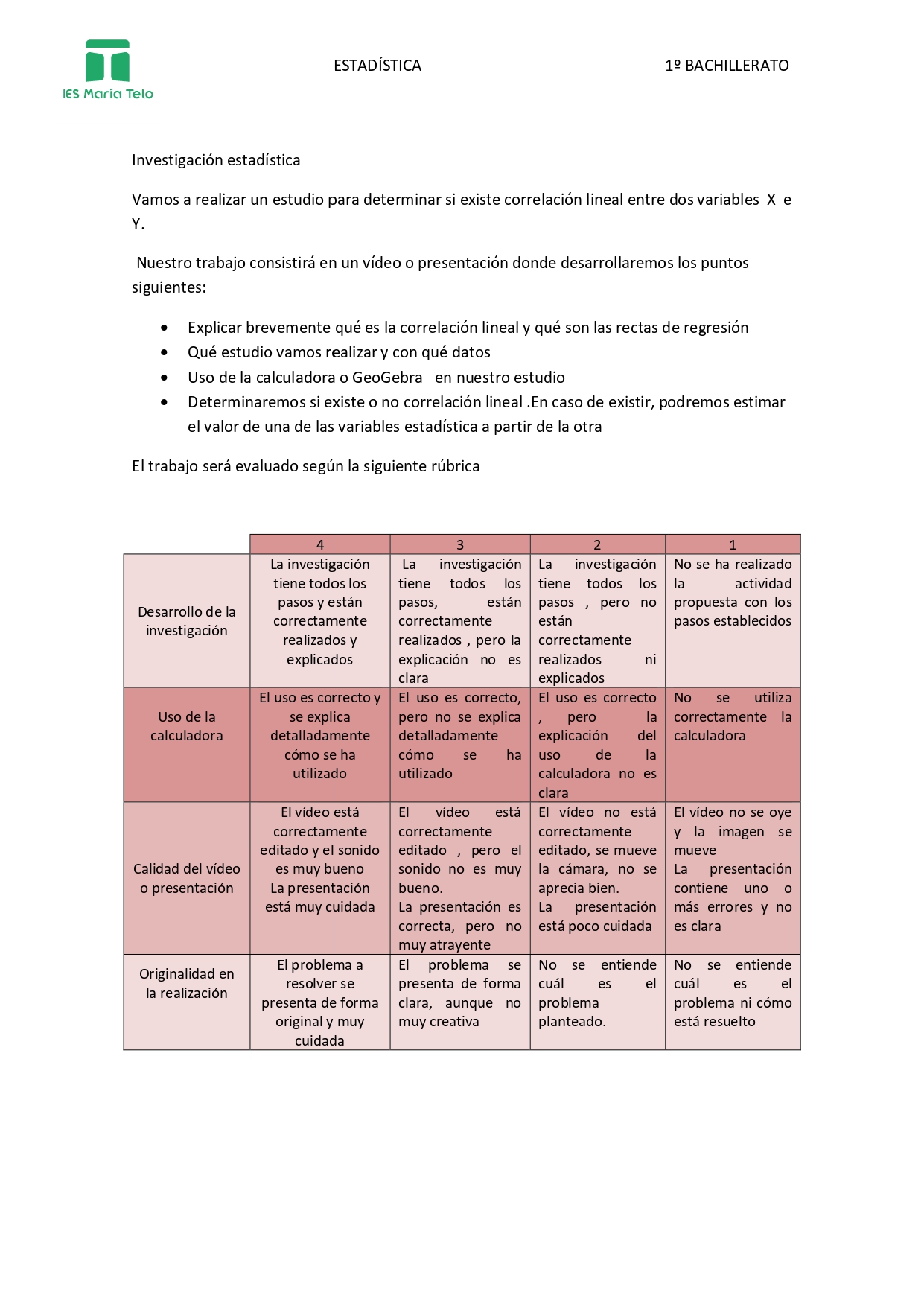
Esta actividad tiene una rúbrica de evaluación que se proporcionó al alumnado y con ella se evalúan criterios relacionados con el aprendizaje colaborativo, en concreto «Trabajar en tareas matemáticas de forma activa en equipos heterogéneos, respetando las emociones y experiencias de los demás, escuchando su razonamiento, aplicando las habilidades sociales más propicias y fomentando el bienestar del equipo y las relaciones saludables.»

El alumnado de atención educativa de 1º de ESO teatralizó » Los números árabes «, dirigido por Silvia Díaz, profesora de Francés, compañera de despacho en la Jefatura de Estudios durante siete años y amiga.

Es posible ( y probable) que el próximo curso también celebre el día π en mi nuevo centro , pero el 14 de marzo de 2024 ha sido inolvidable. A quienes lo habéis hecho posible, muchas gracias.

Problemas de cine

 El trabajo de la primera evaluación del curso 22-23 para 2º A de Bachillerato ha consistido en la realización de un vídeo .

Las Matemáticas son el arte de la explicación, por ello el objetivo perseguido era explicar la resolución de un problema.

Al alumnado se le entrega una ficha de trabajo donde se detalla en qué consiste:

A cada alumno/ a se le ha propuesto un problema diferente, extraído de  https://mathigon.org/puzzles#2021.

La rúbrica de valoración que se facilitó al alumnado en el documento en el que se recogía la estructura del trabajo, es esta:

Una selección de los vídeos se presentó durante la Semana de la Ciencia que celebramos en el Instituto del 14 al 18 de noviembre, con gran éxito de crítica y público.

Bailando sin salir de clase

En Taller de matemáticas de 3º de ESO, este curso 21-22 terminamos el año intentando aprender algo sobre simetrías, giros y traslaciones. Y como este curso estamos profundizando en aprendizaje colaborativo, ¡qué mejor manera que hacer, entre todos, una coreografía!.

En primer lugar intentamos documentarnos y encontramos en Instagram el perfil «Geometrie variable» , que nos sirvió de inspiración. La propuesta que acordamos consistía en » aprender» los movimientos, y después » ensayar» hasta conseguir no equivocarnos mucho.

Los movimientos que acordamos aprender los grabamos en vídeo, que subimos a nuestro equipo de TEAMS

Después , debíamos decidir qué música utilizar; en esto no hubo acuerdo y se editó el vídeo anterior con tres bandas sonoras diferentes, de modo que cada cual practicó con la que prefería.

Como experiencia didáctica es enriquecedora; este curso, en Taller de Matemáticas de 3º de ESO, hay alumnado que cursa Matemáticas académicas, Matemáticas aplicadas y alumnado de 2º PMAR. El grupo es muy heterogéneo y , en general, el nivel de motivación no es alto, por lo que , si bien, el resultado es mejorable, conseguir en dos sesiones aprender los movimientos y repetirlos sin muchos errores, es un muy buen resultado como grupo-clase.

Por cierto, el título de esta entrada parafrasea «Bailando sin salir de casa», título de una canción del grupo Olé Olé del año 1986. Algunos y algunas seguro que recordáis la letra :

«Deberás ser buena alumna
Aburrida como las demás
Pero no tengo la culpa
Las piernas se me van»

El resultado final lo tenéis aquí.

¿ A quién le importan las Matemáticas?

Este curso , en el Instituto, y por iniciativa de mis compañeras de Física y Química y Biología nos hemos decidido a visibilizar la Ciencia, y las Matemáticas ( » llave y puerta de la Ciencia» ) no podían faltar.

Propuse a mi alumnado de Taller de Matemáticas de 3º de ESO, mostrar una construcción GeoGebra que habíamos realizado en el taller y algunos me miraron sorprendidos, porque… «Carmen, ¿a quién va a interesarle semejante cosa?»

Mi intención era mostrar en el patio parte de lo que hacemos en clase y ,una vez más, mi alumnado me sorprendió muy gratamente, porque tuvieron valor y ganas . El alumnado de Taller de Matemáticas de 3º de ESO mostró una construcción con color dinámico y dos alumnas de 2º de Bachillerato nos contaron la práctica realizada en la 1ª evaluación que consistía en » ver» la resolución de un sistema lineal de tres ecuaciones.

¿ Qué tenía de especial esta actividad?

Pues , en primer lugar, hacer Matemáticas en el recreo, en el patio, para todo el mundo, era algo nuevo que no habíamos hecho jamás . Era nuestra » primera vez» y nos enfrentamos ( alumnado y , sobre todo la profe ) con miedo , pero con confianza .

Y en segundo lugar, esa alegría profunda que siento cuando, al «ver» Matemáticas, alguien dice » ¡Qué bonito! » . Aunque no lo diga completamente en serio, me hace sentir que algo está cambiando en la Educación Matemática de nuestro país, a mejor.

View this post on Instagram

A post shared by IES María Telo (@iesmariatelo)

Belleza y romance

«Las matemáticas tienen belleza y romance. El mundo de las matemáticas no es un lugar aburrido en el que estar. Es un lugar extraordinario; merece la pena pasar el tiempo allí.»                                                                                                         Marcus du Sautoy.

 

Dicen que nunca es tarde si la dicha es buena; hace tiempo que quería compartir algunas cosas….

Por una parte los pequeños proyectos  ( pequeñísimos, realmente) que este curso he desarrollado, que se enclavan dentro del plan integrado de innovación educativa que llevamos a cabo en el centro  y que comparto en el siguiente enlace    PIIE 19-20

Y por otra, esos momentos mágicos que me da la docencia………

Este curso para evaluar la parte de probabilidad de 2º de Bachillerato pedí a mi alumnado un vídeo en el que se resolviera un problema asignado previamente. Y recibí  problemas y vídeos  hechos con esmero y atención.

Pero en este, además, hay mucho arte .Gracias Andrea e Irene

Enlace al vídeo

Derivando

Al  alumnado de 2º de Bachillerato   se le propuso la realización de una construcción GeoGebra en la que se mostrara la relación entre la derivada de una función en un punto y la función derivada ; también se buscaba, con esta construcción, reflexionar  sobre el crecimiento de una función y su relación con la función derivada primera.

 La propuesta de esta práctica se realizó por escrito, y se facilitó la rúbrica de valoración. La calificación de esta  práctica formó parte de la nota de cada alumno/a relativa a la actitud y  trabajo en el aula que la programación de nuestro Departamento Didáctico establece para determinar la nota de la primera evaluación del curso 19-20

En el enlace puede accederse a las construcciones realizadas por el alumnado del grupo

Enlace al libro GeoGebra

Que Pitágoras te ilumine

 

Para calificar la parte final de la asignatura Matemáticas I de primer curso de Bachillerato propuse  al alumnado realizar un vídeo sobre una pequeña investigación estadística.

Dos alumnas decidieron  » dramatizar » el trabajo y hacer un pequeño guión. Y me sorprendieron muy gratamente.

 

Aquí os dejo los enlace por si sentís curiosidad

Y Pitágoras aparece

Enlace al vídeo completo

 

 

Quien se atreve a enseñar………

Casi a punto de terminar el curso del INTEF ( Instituto nacional de Tecnologías educativas y de formación del profesorado) sobre ABP en Secundaria

Te esperaré en el límite del bien y del mal

Bernard Bolzano (Praga, Bohemia (actual República Checa) de 1781 –  1848))  fue un matemático, lógico, filósofo y teólogo bohemio que escribió en alemán y que realizó importantes contribuciones a las matemáticas y a la Teoría del conocimiento.

En Matemáticas, se le conoce por el teorema de Bolzano, así como por el teorema de Bolzano-Weierstrass, que esbozó como lema de otro trabajo en 1817, y décadas después habría de desarrollar Karl Weierstrass.

En su filosofía, Bolzano criticó el idealismo de Hegel y Kant, afirmando que los números, las ideas, y las verdades existen de modo independiente a las personas que los piensen.

 

Continuidad en un intervalo

 

 

¡Hola , Cálculo!

Para todos los que » estamos aprendiendo» las reglas de derivación

Hello Calculus!

 

También tenemos un powtoon con los pasos para representar una función.

 

http://www.powtoon.com/embed/bbyH7t9GcAZ/»